У начинающих конструкторов по-прежнему наблюдается потребность в простой и надежной теории расчета силовой установки самодельного летательного аппарата (СЛА) или аэросаней. Необходимые сведения разбросаны по различным журналам и специальным книгам. Кроме того, сравнение опубликованных методик расчета показывает, что иногда они дают несовпадающие результаты как из-за разных исходных принципов, так и из-за различных значений коэффициентов в формулах. В нашем же изложении использованы простейшие физические закономерности и статистические данные о нескольких десятках успешно летавших СЛА, что существенно повышает достоверность и практическое значение приводимых ниже формул.
Какой должна быть тяга винта, чтобы аппарат мог легко взлетать? — вот главный вопрос, который в первую очередь должен решить конструктор, приступающий к проектированию СЛА. Многие неудачи и горькие разочарования происходили только потому, что этот вопрос оставляли на потом, не придавали ему первостепенного значения.
Требуемая для взлета тяга винта F определяется только двумя параметрами: взлетным весом G и минимальным (во взлетном режиме) коэффициентом аэродинамического качества К0:
F=G/K0
Под взлетным весом понимается сумма весов пустого аппарата, летчика, бензина и багажа (груза), а аэродинамическое качество равно отношению подъемной силы крыла к силе лобового сопротивления.
Начинающие конструкторы обычно сильно завышают значение К0 своего будущего аппарата по сравнению с реально достижимым, а также склонны занижать G, поэтому для успеха проекта нужно быть самокритичным и делать предельно жесткие оценки.
По литературным данным о построенных СЛА получается, что будет правильным, если при проектировании принять К0 = 3. Особенно это верно для СЛА, имеющего простейшее «тряпичное» крыло с одинарной обшивкой.
Таким образом, легкий взлет обеспечит силовая установка, создающая тягу F = G/3. Например, при G = 210 кг необходимая тяга составляет 70 кг. Конечно, отрыв от земли может произойти и при меньшей тяге, однако скорость вертикального подъема при этом будет небольшой или вообще аппарат будет только лететь на небольшой высоте, когда действует экранный эффект. Последний немного повышает К0 , и при проектировании, например, экранолета можно принять К0 = 4.
Что касается аэросаней, то для них роль коэффициента аэродинамического качества выполняет величина, обратная коэффициенту трения лыж о снег Ктр. Согласно В.Г.Осташову и Л.Б.Сандперу, Ктр возрастает с увеличением скорости движения и достигает значения примерно 0,2 при V = 50 км/ч (здесь учитывается и относительно небольшое воздушное сопротивление). Следовательно, для «аэросанного» коэффициента качества можно принять значение Ко = 1:0,2 = 5. Если ожидается плохое скольжение, то этот показатель следует понизить до 4.
Как получить необходимую тягу винта?
Тяга (речь пойдет о двухлопастном винте неизменяемого шага) в первую очередь зависит от следующих параметров: мощности мотора N, диаметра D и скорости вращения винта n. Теоретически эти параметры связаны соотношениями, которые легко получить из соображений физической размерности:
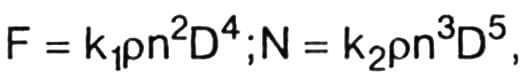
где ρ— плотность воздуха, k1 и k2— безразмерные коэффициенты тяги и мощности. Отсюда после несложных преобразований получаются следующие две формулы:
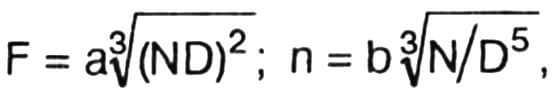
где а и b — некоторые коэффициенты.
Значения а и b были определены автором в результате статистической обработки данных о силовых установках примерно сорока СЛА. Эти данные приведены в техническом отчете о смотре-конкурсе СЛА-87 (издание Сиб.НИИ авиации, Новосибирск, 1990). Оказалось, что в среднем а = 7,5±1, b = 1,6±0,2.
Отклонения от средних значений приведены с 90-процентной вероятностью, то есть 90 процентов «обсчитанных» СЛА имели значения этих коэффициентов в пределах соответственно 6,5 — 8,5 и 1,4 — 1,8. Таким образом, тягу винта и скорость его вращения следует вычислять по формулам:
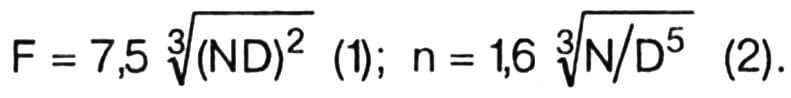
Здесь и далее сила тяги F выражена в кг, мощность мотора N — в л.с., диаметр винта D — в м, скорость вращения винта n — в тыс. об/мин.
Из формулы (1) видно, что тяга винта определяется произведением мощности мотора на диаметр винта. Следовательно, нужную тягу можно в принципе получить и от маломощного мотора, если использовать винт большого диаметра и при этом, согласно формуле (2), понизить/обороты винта.
Расчет силовой установки выполняют в зависимости оттого, чем располагает конструктор для создания своего аппарата. Обычно исходят из того, какой имеется мотор — мотоциклетный, лодочный, от снегохода, мотопомпы, «пускача» дизеля, бензопилы и, в лучшем случае, специальный авиадвигатель для СЛА. Поэтому вначале необходимо выяснить, подойдет ли имеющийся для проектируемого аппарата?
Пусть, например, есть мотор с фактической (или паспортной, если он новый) мощностью N = 10 л.с., а требуемая тяга винта составляет 70 кг. Спрашивается, какими должны быть диаметр винта и скорость его вращения, чтобы получилась нужная тяга? Диаметр винта находим из формулы (1):
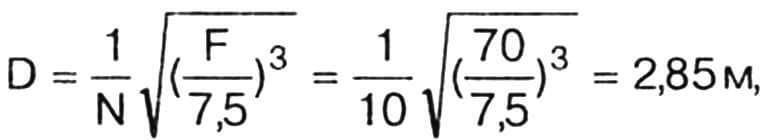
а скорость вращения — по формуле (2):
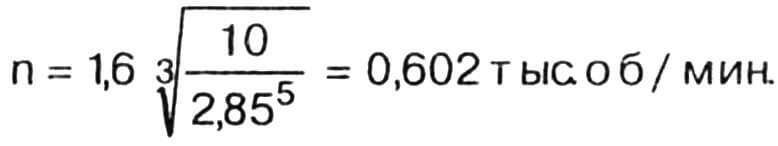
Таким образом, данный мотор потребует использования очень большого (по меркам СЛА или любительских аэросаней) винта, который к тому же должен вращаться с весьма небольшой скоростью, что, в свою очередь, приведет к необходимости сложного многоступенчатого редуктора, так как обороты коленчатого вала мотора обычно составляют 5—6 тыс. об/мин. В результате получится громоздкая и утяжеленная силовая установка, поэтому от такого мотора лучше отказаться.
Можно при проектировании исходить и из габаритных соображений. Например, пусть по проектным габаритам силовой установки диаметр винта не должен превышать 1,5 м. Требуемая тяга винта составляет 70 кг. Какими при этом должны быть мощность и скорость вращения винта? Из формулы (1) N = 19 л.с., а по формуле (2) п = 2,172 тыс. об/мин.
Подходящими для этого варианта моторами могут быть некоторые лодочные («Привет-22», «Москва-25» и др.) и мотоциклетные («ИЖ-Юпитер» и др.), при этом должен быть использован редуктор, обеспечивающий расчетные обороты винта.
Изготовление редуктора в любительских условиях — дело сложное и не вполне надежное, поэтому нужно стремиться использовать редуктор заводского производства. Например, в мотоциклетном моторе уже имеется подходящий редуктор — в виде цепной или зубчатой передачи от коленчатого вала к муфте сцепления. Пусть, например, имеется новый мотор «ИЖ-Ю-5» с N = 24 л.с., а его редуктор n = 2,3 тыс. об/мин. Требуемая тяга по-прежнему составляет 70 кг. Из формул (1) и (2) находим, что данные мотор и редуктор обеспечат тягу F = 82 кг (которая даже существенно больше требуемой, что всегда полезно) при диаметре винта D = 1,52 м.
Следует отметить, что если имеется очень мощный мотор, а диаметр винта невелик, например, D = 1 м, то при этом невозможно получить очень большую тягу. Объясняется это ограничением линейной скорости конца лопасти, которая не должна превышать 220 м/с — при большей скорости проявляется звуковой барьер и КПД винта падает. Следовательно, скорость его вращения должна быть ограничена условием n<4,4<D.
Например, при D = 1 м скорость вращения винта не должна превышать 4,4 тыс. об/мин. При этих значениях D и n потребляемая винтом от мотора мощность составит 21 л.с., а тяга будет около 57 кг.
Может случиться так, что имеющиеся мотор и редуктор могут дать тягу, меньшую потребной всего на 10—15 процентов. В таком случае можно все же получить нужную тягу, если заменить 2-лопастный винт 4-лопастным. Теория показывает, что такая замена (при прежних N и n) приводит к увеличению тяги на 15 процентов и к уменьшению диаметра винта на те же 15 процентов.
Наконец, для повышения тяги можно использовать схему «винт в кольце», но при этом надо учитывать, что конусообразное кольцо вокруг винта сделает силовую установку более громоздкой и немного утяжелит ее. Подробнее о схеме «винт в кольце» можно узнать в книге В.Г.Осташова и Л.Б.Сандлера «Глиссирующие снегоходы-амфибии», Новосибирск, 1991.
Геометрия винта
Упрощенный расчет винта заключается в нахождении только установочных углов φ (R) сечений лопасти в зависимости от их удаления (R) от оси вращения винта. Сила тяги, диаметр винта и скорость его вращения должны быть определены предварительно. Винт целесообразно рассчитывать для режима взлетной скорости СЛА, которая находится по формуле:
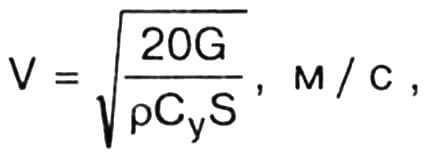
где G — взлетный вес, кг; ρ = 1,25 кг/м3 — нормальная плотность воздуха; Су= 1,4 — средний для СЛА коэффициент подъемной силы крыла во взлетном режиме; S — площадь крыла, м2. Например, при весе G = 210 кг и площади S=15 м2 получаем скорость V = 46 км/ч.
В случае аэросанного винта в качестве расчетной V следует использовать «крейсерскую» скорость движения аэросаней.
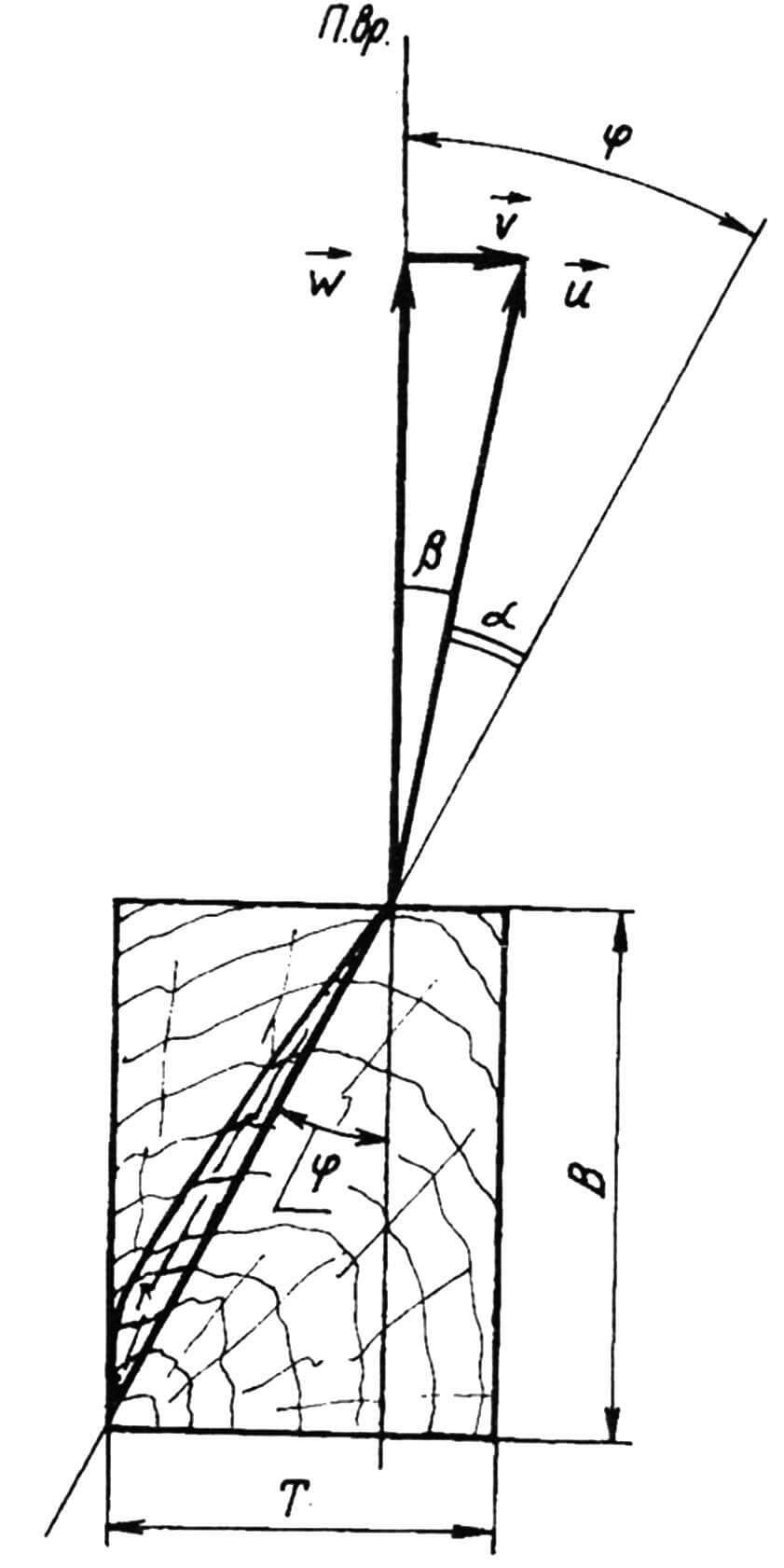
Профили сечений лопасти винта принимаются, как обычно, плосковыпуклыми (плоская сторона — рабочая, выпуклая— тыльная). Тогда установочным углом φ (R) будет угол между плоской стороной лопасти в данном ее сечении и плоскостью вращения винта. Из рисунка видно, что установочный угол больше угла атаки α на угол β, определяемый по формуле:
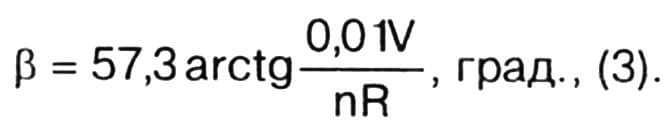
Здесь V выражена в м/с, n — в тыс. об/мин, R — в м.
Расчет по приводимой методике предполагает также знание предельного угла атаки, выше которого происходит срыв потока на некотором участке лопасти и винт перестает хорошо работать. Величина этого угла зависит от используемого профиля сечений. Согласно упомянутой книге Осташова и Сандлера, можно рекомендовать профиль RAF-6, у которого предельный угол атаки около 18°.
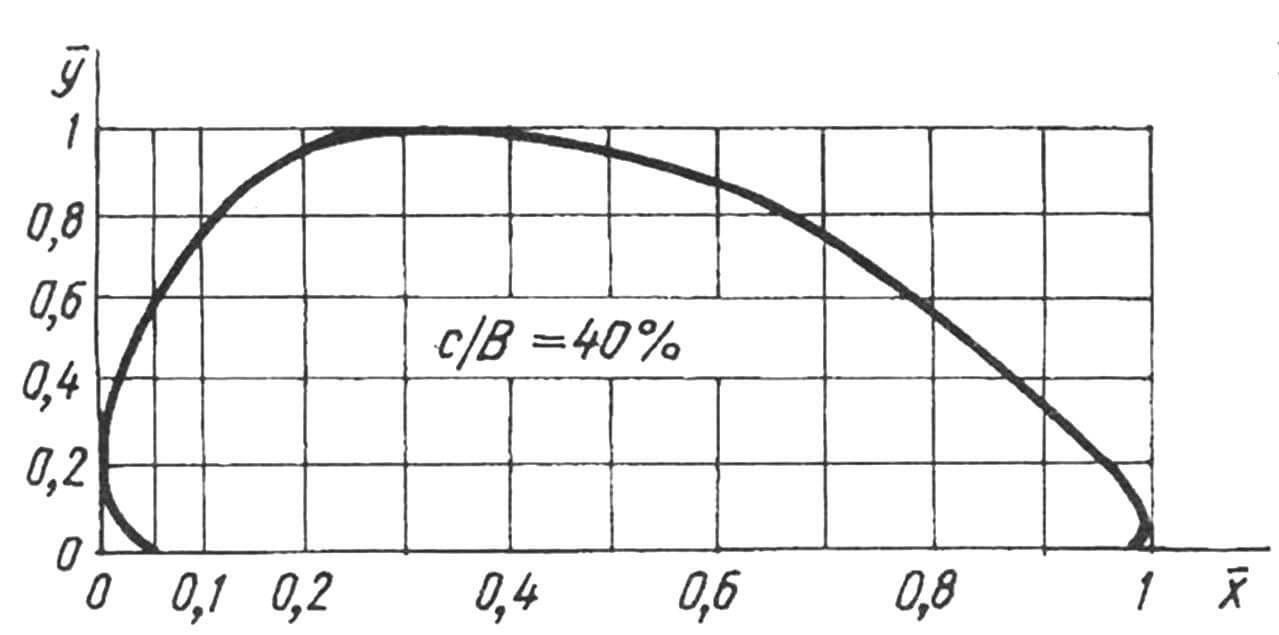
Винт изготавливают из прямоугольного деревянного (ель, береза и др.) бруса длиной D, толщиной Т и шириной В. При этом ширина (хорда) лопасти B(R) в каком-либо ее сечении будет равна B/cos φ (R). Для упрощения расчета можно принять B(R) = В = const, так как установочные углы φ (R) сравнительно невелики (8—30°) и поэтому cos φ (R) = 1. Отношение максимальной толщины профиля (с) к его хорде, то есть с/В принимается в пределах 8—30 процентов с плавным увеличением от 8 на конце лопасти до 30 процентов у ступицы винта.
Чтобы найти угол φ в каком-либо сечении, необходимо по отдельности вычислить углы α и β и затем их сложить. Угол атаки α (R) можно найти из условия постоянства удельной тяги ρ по размаху лопасти на расчетном ее участке:
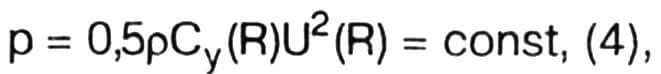
где Cy(R)=4,8 [α(R)+0,0175] — коэффициент «подъемной силы» (то есть тяги данного сечения), связанный с углом атаки α(R), выраженным в радианах, а U2(R)=104n2R2+V2, м2/с2 — квадрат скорости потока воздуха, набегающего на данное сечение лопасти (для наблюдателя, как бы вращающегося вместе с винтом). Понятие «удельная тяга» аналогично «нагрузке на крыло» и показывает, сколько килограммов тяги приходится на единицу площади расчетного участка лопасти. Удельная тяга в данном случае — то же самое, что и давление воздуха, и условие (4) тогда означает, что перепады давления по размаху лопасти отсутствуют и что теоретически должно повышать КПД винта.
С учетом этого из (4) получаем следующее уравнение для вычисления углов атаки:
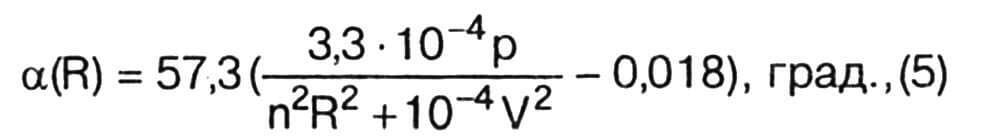
Здесь ρ выражено в кг/м2, n — в тыс.об/мин, R — в м/с.
Из-за существования предельного угла атаки условие (4) нельзя выполнить на всей лопасти, но можно на половине ее размаха — от конца, где R=D/2, до сечения, где R=D/4. Следовательно, расчетный участок лопасти будет иметь длину ΔR=D/4 и площадь ΔR•B=DB/4. Тогда удельная тяга 2-лопастного винта найдется по формуле:
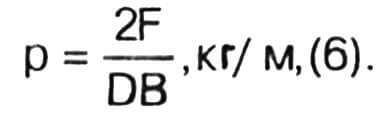
Рассмотрим конкретный пример: определить установочные углы сечений винта диаметром D = 1,5 м, который при n = 2,3 тыс. об/мин, В = 0,12 м, V = 15 м/с и предельном угле атаки в 1 8° должен создавать тягу F = 78 кг.
Вначале по формуле (6) получаем удельную тягу ρ = 867 кг/м.
С учетом данных значений ρ, n и V формулы (3) и (5) приводим к удобному для вычислений виду:
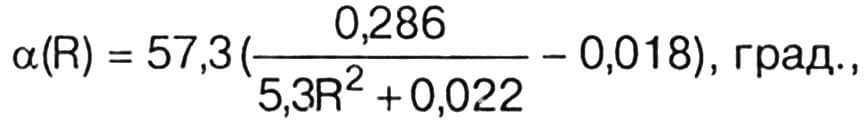
![]()
Углы α, β и φ = α + β вычисляем для следующих значений R: 0,75 (конец лопасти); 0,7; 0,6; 0,5; 0,4; -0,375 (конец расчетного участка). Результаты записываем в таблицу:
| R, м | 0,75 | 0,7 | 0,6 | 0,5 | 0,4 | 0,375 |
| α, град. | 4,45 | 5,25 | 7,5 | 11,2 | 17,8 | 20,4 |
| β, град. | 4,90 | 5,30 | 6,2 | 7,4 | 9,2 | 9,8 |
| φ, град. | 9,35 | 10,6 | 13,7 | 18,6 | 27,0 | 30,2 |
Как видно, предельный угол атаки 18° достигается на конце расчетного участка, примерно при R = 0,4 м. Если бы этого не произошло, то пришлось бы повторить расчеты при другом значении ширины лопасти В, изменяя ее в соответствующую сторону по сравнению с первоначально принятым значением 0,12 м.
Определение установочных углов на оставшемся участке лопасти от R = 0,4 м до R = 0,1D = 0,15 м проводим по формуле:
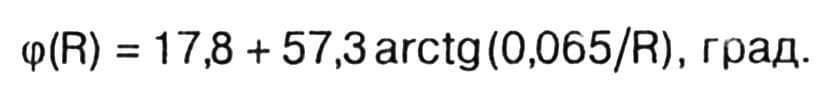
и для R=0,3; 0,2 и 0,15 м получаем соответственно следующие значения угла φ, град: 30,0; 35,8 и 41,2.
Следует отметить, что на втором участке нет особой необходимости в получении больших установочных углов, так как требуемая тяга уже обеспечена на первом расчетном участке. Поэтому, исходя из удобства изготовления винта, можно при R = 0,4…0,15 м принять φ(R) в пределах 27—30°. Это существенно уменьшит толщину Т заготовки (деревянного бруса), так как Т = В tgφmax. Например, при угле φmax = 30° имеем толщину Т = 12 tg30°= 6,9 см, зато при φmax= 41,2° будем иметь Т = 10,5 см.
Приведенная методика расчета винта не является единственно возможной. Например, часто расчет установочных углов ведут из условия постоянства шага винта Н:
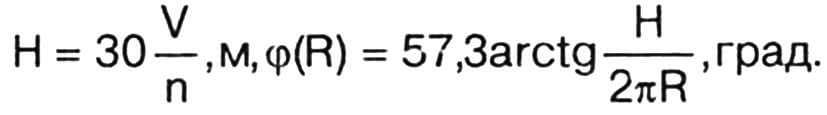
Интересно сравнить, насколько будут отличаться рассчитанные по этой — «шаговой» методике установочные углы от тех значений, что были найдены выше. В примере, который мы рассматривали, V = 15 м/с или 54 км/ч, n = 2300 об/мин и для шага винта по этим формулам Н = 0,704 м, соответственно которому получаются следующие значения установочных углов:
| R, м | 0,75 | 0,7 | 0,6 | 0,5 | 0,4 | 0,375 |
| φ, град | 8,5 | 9,1 | 10,6 | 12,6 | 15,6 | 16,6 |
Из сравнения с предыдущей таблицей видно, что хорошее совпадение значений φ наблюдается при больших R, то есть у конца лопасти. При уменьшении R возникает существенное различие — по «шаговой» методике крутка лопасти получается меньшей, чем по «тяговой» методике (под круткой понимается изменение φ по мере изменения R).
Конечно, правильность расчета винта в итоге могут показать только его тяговые испытания. «Тяговая» методика расчета обладает преимуществом ввиду физической ясности ее основ, в частности, ясным пониманием роли ширины лопасти В: при ее изменении изменяется и удельная тяга, соответственно другими будут углы атаки и установочные углы. В «шаговой» же методике ширина лопасти никак не влияет на установочные углы.
В заключение следует отметить, что единственный построенный по расчету винт только в редких случаях может дать нужный результат. Поэтому следует изготовить несколько винтов, отличающихся установочными углами, и затем в ходе испытаний выбрать из них наилучший.
Б. КАЛЕГАНОВ