ПАРАДОКС ЛЕГКОЙ МОДЕЛИ

«Самая заветная мечта — высота, высота…» Так поется в известной песне о летчиках. Высота — заветная мечта и моделистов-ракетчиков, в каком бы классе соревнований ни выступал спортсмен. Для «высотных» моделей это прямая цель, а планирующим и парашютирующим набранная высота гарантирует хорошую продолжительность полета.

Спросите любого моделиста, что нужно сделать, чтобы модель поднялась на наибольшую высоту, и в числе многих правильных ответов — уменьшить аэродинамическое сопротивление, поставить двигатель с большей удельной тягой, обеспечить хорошую стабилизацию полета — и других наверняка будет и такой: «Сделать модель как можно легче». Казалось бы, правильно, но на самом деле очень легкая модель может летать так же плохо, как и сравнительно тяжелая. Назовем это интересное явление «парадоксом легкой модели» и попробуем разобраться в его причинах.

Модель ракеты относится к классу неуправляемых баллистических ракет. Траектория их полета состоит из двух основных участков: активного, на котором работают двигатели, и пассивного, на котором ракета летит подобно камню, брошенному древней метательной машиной — баллистой. Траекторное движение ракеты является результатом воздействия на нее разных сил. Какие же силы действуют на ракету в полете!

Обратимся к авторитету, которому самому довелось испытать эти силы. Послушаем, как отвечает на вопрос о том, с какими силами приходится иметь дело ракете, второй советский посланник в космос — Герман Степанович Титов:

«Во-первых, с тягой двигателя, во-вторых, с силой сопротивления воздуха и, наконец, с весом ракеты. Между этими сипами, образно говоря, идет борьба: тяга двигателя влечет ракету вперед, сопротивление воздуха препятствует ее движению, а вес ракеты тянет вниз. В полете величины этих сил изменяются. Меняется и направление их действия».

От того, какие силы будут иметь перевес, зависит движение ракеты и ее конечный результат — траектория полета.

Силы, действующие на ракету, на активном и пассивном участках различны. В первом случае на вертикально взлетающую модель действует сила тяги двигателей, направленная вверх и разгоняющая ее, а также силы тяжести и аэродинамического сопротивления, тормозящие движение ракеты и направленные вниз. Во втором — остаются только две силы: сопротивления и тяжести.

Наиболее сложен при анализе полета активный участок траектории: на нем изменяются не только силы, но и масса ракеты. Вырабатывая топливо, многие современные ракеты изменяют свою массу в несколько раз.

Изменение массы ракеты в процессе ее движения не позволяет использовать непосредственно те формулы, которые получены в классической механике Ньютона. В наиболее полном и строгом виде подход к изучению движения тел переменной массы был впервые рассмотрен известным русским

механиком И. В. Мещерским. В своей магистерской диссертации «Динамика точки переменной массы», написанной в 1897 году, он получил строгие уравнения движения тела переменной массы при различных гипотезах отбрасывания масс. Независимо от Мещерского применительно к ракетам исследовал движение тела переменной массы К. Э. Циолковский. Теорию движения ракеты теперь называют ракетодинамикой, а Циолковского по праву считают основоположником современной ракетодинамики.

Размышляя о тайнах полета ракеты, Циолковский шел глубоко научным путем, последовательно вводя основные силы, от которых зависит движение ракеты. Чтобы выяснить возможности самого реактивного принципа перемещения тел, ученый рассмотрел простейшую задачу-предположение: полет ракеты, на которую действует только сила тяги. Эта задача сейчас называется первой задачей Циолковского. Один из ее важнейших выводов гласит, что для одноступенчатой ранеты скорость в конце активного участка будет тем больше, чем больше отношение масс в начале и в конце полета.

Графический метод определения высоты полета.

Во второй задаче Циолковский рассмотрел вертикальный подъем ракеты с Земли, лишенной атмосферы. Анализ показал, что высота активного подъема ракеты тоже будет расти при увеличении отношения ее начальной массы и конечной.

Реальный полет ракеты в воздушной среде усложняет задачу настолько, что получить решение в виде простых формул не удается, и достаточно точно рассчитывать движение ракеты под действием всех трех сил научились сравнительно недавно, используя «счеты XX века» — электронные вычислительные машины. Однако качественно выводы первой и второй задач Циолковского остаются справедливыми для вертикального подъема ракеты или модели в атмосфере: с ростом отношения начальной и конечной масс увеличиваются как скорость, так и высота в конце активного участка траектории.

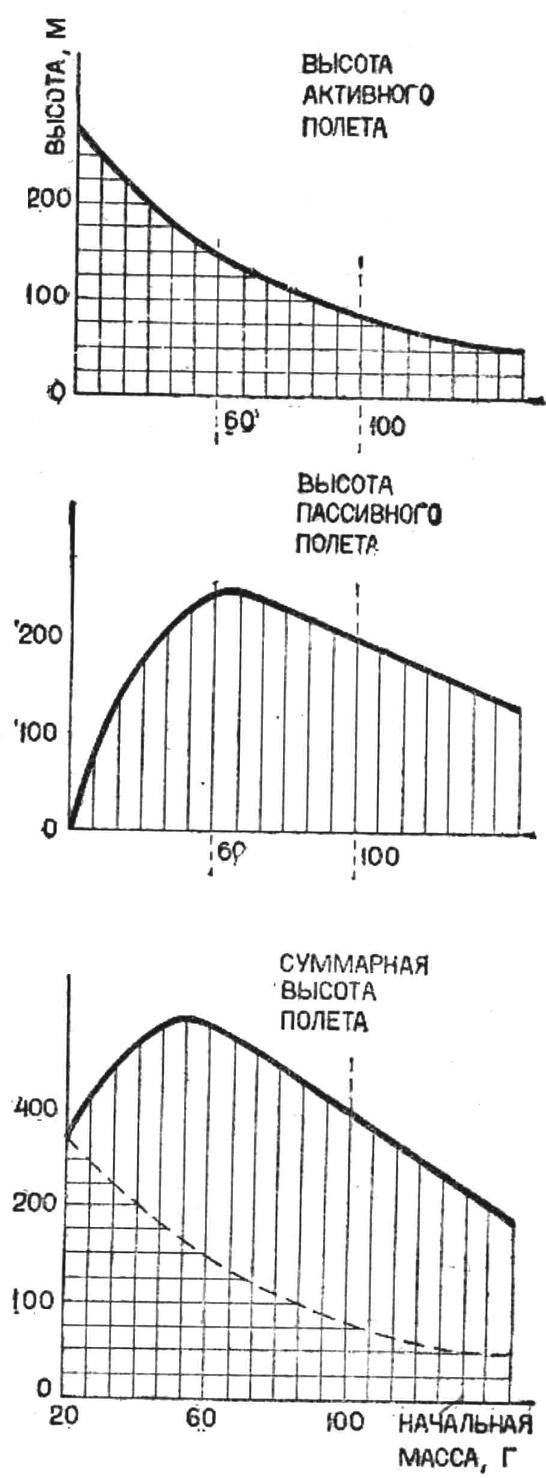
Для иллюстрации приведем результаты расчета высоты подъема моделей, имеющих разные веса при старте (см. рис.). Траектория полета рассчитывалась путем решения сложных дифференциальных уравнений на электронной вычислительной машине. Для расчета была взята одноступенчатая модель с диаметром мидельного сечения 22 мм и коэффициентом лобового сопротивления 0,75. Двигатель модели имеет полный импульс 10 Н·с и создает реактивную силу 5 Н в течение двух секунд. Масса топлива в двигателе составляет 20 г. Начальную массу при расчете изменяли, чтобы сравнить высоту подъема моделей.

График А показывает высоту активного полета. При увеличении начальной массы ракеты и постоянной мессе топлива отношение начальной и конечной масс уменьшается. Так, для начальной массы 40 г это отношение равно 2, а для 100 г —1,25. Соответственно высота активного подъема в первом случае составляет 200 м, а во втором — 85 м, а скорости в конце активного участка — 160 м/сек и 84 м/сек.

Таким образом, облегчение модели ведет к увеличению высоты активного полета, и наибольшей эта высота станет, если вся ракета будет состоять из одного топлива, то есть иметь массу на старте 20 г. Конечно, этот вариант нереален, но он представляет интерес как предельный случай самой легкой модели. По графику для такой сверхлегкой модели высота активного подъема достигает 245 м.

Предельным случаем сверхтяжелой модели, когда ракета вообще не сможет взлететь, является вариант, при котором конечный вес модели будет больше тяги двигателя. Расчетная модель, например, не взлетит при начальной массе более 500 г.

Обратимся теперь к пассивному участку траектории (график Б]. Как влияет на высоту баллистического полета облегчение или утяжеление модели? На этом участке масса ракеты постоянна и равна конечной (начальной массе без топлива). Здесь можно воспользоваться вторым законом Ньютона, которым гласит, что ускорение тела пропорционально силе, действующей, на него пропорционально массе.

Очевидно, что подъем ракеты на пассивном участке будет тем выше, чем меньшее ускорение испытывает она под действием сил тяжести и воздушного сопротивления. Ускорение гравитационных сил в пределах высот подъема моделей можно считать постоянным. При одном и том же сопротивлении ракета, имеющая большую массу, будет испытывать меньшее ускорение и поднимется на большую высоту.

Итак, более тяжелая ракета при постоянной скорости в конце активного участка имеет более протяженный участок пассивного подъема. Но, к сожалению, нужно учитывать, что с утяжелением ракеты конечная скорость ев активного полета снижается. Под действием этих двух факторов высота пассивного подъема с ростом начальной массы сначала увеличивается, а затем уменьшается. Для расчетной модели высота пассивного подъема станет наибольшей при стартовой массе, равной 65 г.

Интересно отметить, что «сверхлегкая» модель совсем не имеет пассивного участка. Помните загадку? «Что может поднять младенец, а силач и через ручей не перебросит?» Ответ: «Пушинку». Действительно, попробуйте бросить пушинку: далеко она не полетит, как бы сильно ее ни бросали. Так и для модели. Если выполнить ее слишком легкой, высоко она не поднимется, какую бы скорость ей ни сообщали в конце активного участка.

Значит, облегчая модель, мы практически лишаем ее возможности пассивного полета, утяжеляя — ухудшаем условия и результат (конечную скорость и высоту) активного полета. Между этими двумя крайними случаями где-то находится «золотая середина» модель, обладающая оптимальной начальной массой. Эту массу можно определить для расчетной модели по графику В, где представлена суммарная высота активного и пассивного участков полета. Она составляет 53 г, а высота ее подъема равна 395 м. Более легкие и более тяжелые модели имеют меньшую высоту. Одинаковые высоты можно получить и для легких, и для тяжелых ракет. Например, высоту 345 м можно получить для моделей с начальными массами 30 г и 90 г.

Итак, явление «парадокса легкой модели» приводит нас к выводу, что не всегда нужно стремиться облегчать модель: уменьшение массы модели сверх оптимального значения не дает выигрыша в высоте. Поиски оптимального значения стартовой массы своей модели — одна из задач ракетомоделиста, решение которой позволит добиться ему наилучших результатов в соревнованиях.

В. КАНАЕВ, инженер