Судя по письмам, пришедшим в редакцию после опубликования статьи в «М-К» № 6 и 7 за 1988 год, попытки создать обоснованную теорию полета кордовых моделей привлекли внимание многих наших читателей-авиамоделистов. Включение момента инерции в расчет потенциальных маневренных свойств заинтересовало не только спортсменов-бойцов, но и пилотажников.
Рады отметить, что их интерес оправдан практичностью предложенных приемов расчета, а не одной лишь необычностью рассматриваемых понятий. Надеемся, не меньшую пользу принесет и сегодняшняя публикация, содержащая столь же нетрадиционный подход к «математизации» узлов, кажущихся простыми в проектировании.
Тема сегодняшнего разговора — расчет системы управления бойцовой (а в принципе и пилотажной) кордовой моделью, включающей в себя все элементы: от ручки управления до кабанчиков рулей и закрылков в варианте пилотажного аппарата.
Скорее всего постановка подобного вопроса поначалу вызовет по крайней мере недоумение. Особенно когда придется уточнить: ни передаточное отношение, ни прочностно-жесткостные проблемы (хоть и весьма важные, но легко решаемые) сегодня нас не интересуют. Тогда что же рассчитывать и зачем? А вот в этом и нужно разобраться.
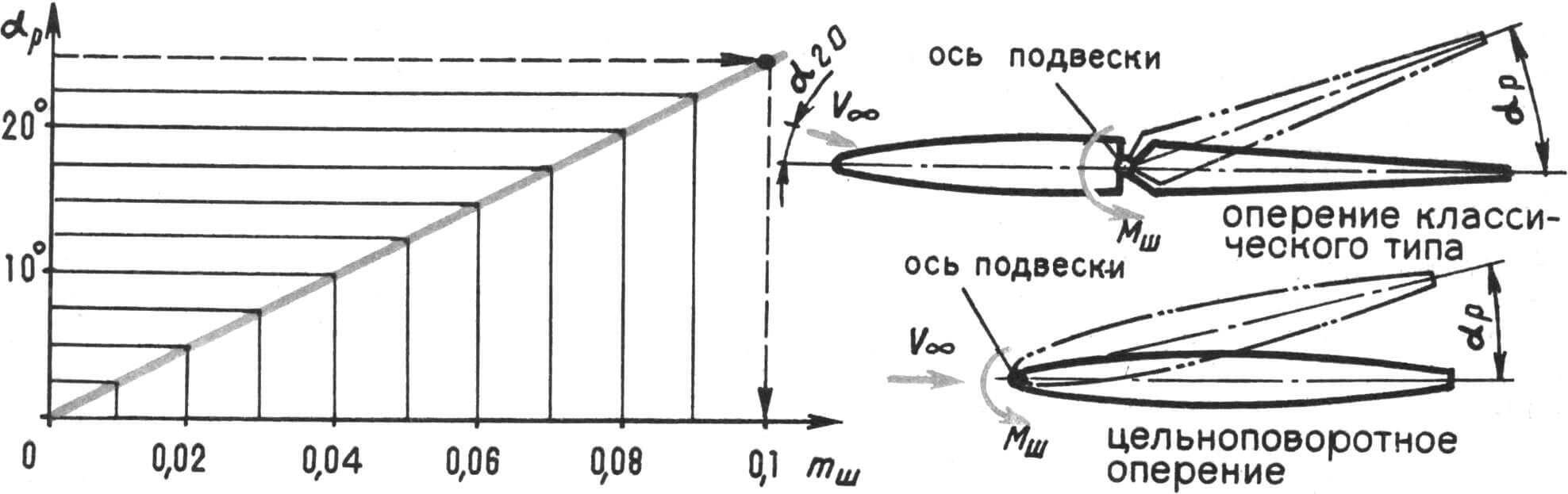
Справа показана схема оперения, для которой обеспечивается данная зависимость (хорда руля равна хорде неподвижной части оперения, угол атаки оперения равен нулю, точка подвеса руля — на его передней кромке).
Ручка управления нас интересует лишь как рычаг, задающий «дозированные» перемещения кордовых нитей относительно друг друга. Сами нити в нашем разговоре интересны как… пружины, но об этом чуть позже, а начнем мы с рассмотрения качалки. Нам понадобится в первую очередь определить ее «размах» — расстояние между точками подвеса тросиков. Как правило, этот размер выбирается исходя из компоновочных соображений или же на базе статистических данных. На деле же «размах» качалки в каждом конкретном случае должен рассчитываться: от его размера во многом зависит управляемость!
Прежде-всего уточним, на что влияет «размах» и каким образом. А для этого нужно ввести непривычное для моделистов, но хорошо известное в аэродинамике понятие — шарнирный момент. Фактически это момент силы, который необходимо приложить к точке навески рулевой поверхности для поворота на заданный угол в каких-то данных условиях (угол атаки всего оперения, скорость обтекания оперения и другое). Величина момента рассчитывается так:
Mm=mm*SpBp*qp, где
Mm — искомый момент, кгс*м, mm — безразмерный опытный коэффициент,
Sp — площадь рулевой поверхности, м2,
Вр — средняя хорда рулевой поверхности, м, qp — скоростной напор в зоне расположения рулевой поверхности, кгс/м2.
Скоростной напор в наших расчетах можно принять равным для невозмущенного набегающего потока, а торможением потока за крылом и увеличением эффективности рулей в потоке за воздушным винтом мы пренебрегаем. Тогда для стандартных атмосферных условий:
qp=qs=0,06 V2, где
V — скорость полета модели, м/с.
Что, замысловато? Но не поленитесь и проследуйте до конца с нами в рассуждениях. Обещаем — выводы будут очень занятны, а все расчеты упростятся до элементарных, тем более если вы занимаетесь моделями одного класса.
Итак, для нахождения шарнирного момента есть все величины, кроме безразмерного коэффициента. Его легко найти, воспользовавшись графиком (рис. 1). Конкретизировав задачу, уже сейчас можно ее упростить. Достаточно одну максимальную скорость выбрать раз и навсегда, просчитать для нее скоростной напор и задаться одним «типовым» углом отклонения руля.
Теперь возьмем геометрические данные для, например, модели воздушного боя или для пилотажной (в последнем случае нужно учесть, конечно, как рули высоты, так и закрылки) и найдем шарнирный момент всех рулевых поверхностей. Готово? Проверьте расчеты еще раз — возможна ошибка из-за перевода линейных размеров деталей и площадей в непривычные для моделистов метры и м2. Порядок получаемых величин можно представить на примере модели воздушного боя: руль высоты размером 50X250 мм подвешен на передней кромке, скорость полета 150 км/ч (42 м/с), максимальный угол отклонения руля 25°, откуда после пересчета Мm=0,006—0,007 кгсХм. Переведя момент в привычные величины, имеем Мm=0,6—0,7 кгсХсм.
Сразу же параллельно отметим, что полученное значение дает представление о силах, возникающих в тягах рулей как при их растяжении, так и сжатии. При кабанчике высотой 10 мм это 0,6—0,7 кгс, что заставляет задуматься об устойчивости тонкого стержневого элемента. Причем лишь двойное увеличение размеров руля приводит к восьмикратному росту Мm!
Но главное не в этом. Мучились мы с подобной «арифметикой» ради нахождения минимального натяжения корд, необходимого для поворота руля на заданный угол. Получить искомую величину теперь несложно — надо шарнирный момент разделить на полуразмерах качалки управления (соответственно выраженный в метрах или сантиметрах). Поправки нужно ввести только при значительной разности кабанчика и управляющего плеча качалки. В приведенном примере при размахе качалки 50 мм минимальное натяжение корд, когда уже модель практически повисает на одной лишь нити, оказывается равным 0,24—0,28 кгс. Много это или мало? Если говорить о моделях опытных спортсменов, то достаточно. А в других вариантах… Ведь на найденную величину влияние оказывает множество факторов: порыв ветра, на мгновение увеличивший фактическую скорость «обдувки»; значительное сопротивление завившихся после нескольких фигур кордовых нитей; ослабление натяжения при полете «в зените» или при том же порыве ветра… Все только повышает требования к точности прохождения «сигнала» от ручки к качалке.
Особо надо отметить влияние Мm на фактор, принятый называть «ветрозащищенностью». Несмотря на расплывчатость и неопределенность последнего понятия, ясно, что при нехватке натяжения корд руль в порывах вероятнее всего будет плавно уходить от заданного положения под воздействием возросшей аэродинамической нагрузки. Но пилот заметить это не в состоянии, он увидит лишь результат — уход модели с заданной траектории! Тогда, может быть, такой эффект и есть определяющий «ветрозащищенность»? По крайней мере для пилотажных аппаратов, где располагаемый управляющий момент очень близок к суммарному шарнирному, любой недостаток натяжения будет проявляться именно в условиях порывов ветра.
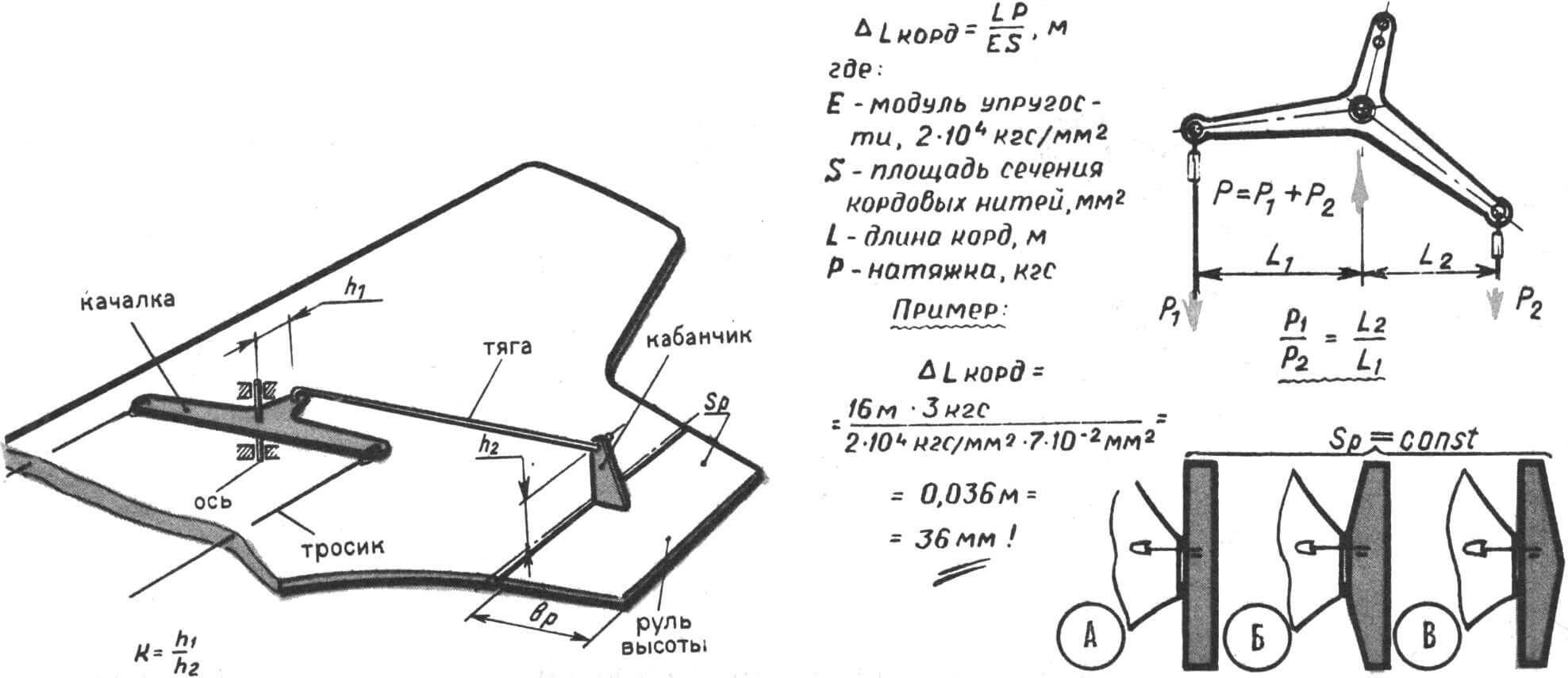
A — обычная форма, Б — модификация, увеличивающая шарнирный момент, В — модификация, снижающая шарнирный момент.
А как обстоят дела в избранном нами примере? Элементарная прикидка центробежной силы в горизонтальном полете дает натяжение, в лучшем случае не превышающее 0,4 кгс при массе бойцовой 0,4 кг! Значит, запас по натяжению равен всего лишь 0,12—0,16 кгс! Вспомните, сколько негативных факторов присутствует в полете модели, добавьте к этому перечню еще и почти двукратное увеличение Мm при выходе неподвижной части горизонтального оперения на большие углы атаки (график соответствует нулевому углу атаки стабилизатора), как станет ясно: и для бойцовых моделей проблема управляемости так же важна, как и для пилотажных. Правда, у «летающих крыльев» все не так критично. Здесь сказываются малые углы отклонения рулей, а соответственно и введение поправок на соотношение длин кабанчика и- управляющего рычага качалки, да и выход крыла на фигуре на углы, обратные углам отклонения руля, также смягчает условия работы системы управления. Но стоит поставить качалку с малым «размахом», снизить массу модели или установить на нее руль большой площади, как проблема станет очень близкой к реальным условиям.
В окончании разговора о шарнирных моментах надо лишь уточнить, что приведенные зависимости правомерны… для всего диапазона скоростей полета конкретной модели! Ведь при росте или снижении центробежной силы точно в такой же пропорции меняется и Мm!
Выводы однозначны. Как стало понятно, качалку рассчитывать нужно. А в качестве мер по повышению точности управления любой кордовой моделью можно рекомендовать использование увеличенных качалок (только по «размаху», причем с сохранением углов отклонения от нейтрали, для чего придется применять и увеличенные ручки), подбирать оптимальную массу модели (от нее зависит напрямую центробежная сила) и не забывать о таком приеме, как аэродинамическая компенсация рулей, широко известная в авиации.
Системы управления касается и вопрос «стреловидности» качалки. В ряде публикаций в иностранных журналах можно встретить упоминание о подобных деталях, якобы повышающих устойчивость либо управляемость аппаратов. Рекомендуем крайне критически отнестись к таким материалам! Практические точные построения кинематики таких качалок по крайней мере не подтверждают заявленных изменений характера передачи сигнала от ручки к рулям. Кроме того, как показали испытания специально построенной экспериментальной модели с качалками всевозможных стреловидностей, за счет лишь небольших изменений данного параметра можно из абсолютно «тупого» аппарата без любых других приемов получить «сверхострый» и неустойчивый! Чтобы правильно понять воздействие стреловидности качалки на характер управления, достаточно обратить внимание на разность плеч приложения усилия натяжки тросиков управления относительно центральной оси. В результате натяжение перераспределяется по закону рычагов, и появляется разность удлинений кордовых нитей. А ведь в ряде случаев эта разность может по величине приближаться ко всему ходу качалки! Если вас затруднят расчеты удлинений нитей, советуем испытать на любой модели две качалки — с прямой и обратной стреловидностью порядка хотя бы 20° на сторону. Полученный даже на легком аппарате эффект убедит вас в необходимости установки исключительно прямых элементов управления.
В. ОЛЬГИН