Можно поставить на автомобиль 4, 8… даже 16 колес. Однако в тундре, например, даже такая машина не пройдет и километра. И неудивительно, что целые конструкторские коллективы занимаются поисками новых движителей, которые пришли бы на смену колесу и обеспечили «всепогодную» доставку грузов, трелевку леса, работу поисковых партий… Уже созданы для этого образцы гусеничных машин с широченными, чуть ли не в 1,5 м траками, шнекоходов, судов на воздушной подушке.
Не отстают в своих творческих поисках и юные техники; причем они предлагают порой даже более смелые решения, чем те, что рождаются во «взрослых» КБ. Один из примеров этого — модель тундрохода «Жук», представленная на «Конкурс идей» юными техниками Магаданской СЮТ. Это безгусеничный вездеход, движителем которого является шагающее устройство.
Щелкает тумблер, и модель, внешне напоминающая божью коровку, начинает быстро перебирать ножками. Она не только движется, но и преодолевает различные препятствия.
Основа модели — две пары секторов. Если посадить их на общую ось, то, как нетрудно убедиться, перемещение вперед можно производить двумя способами — вращая поочередно секторы вокруг оси (рис. 1) или двигая их один за другим, как бы шагая (рис. 1. В).
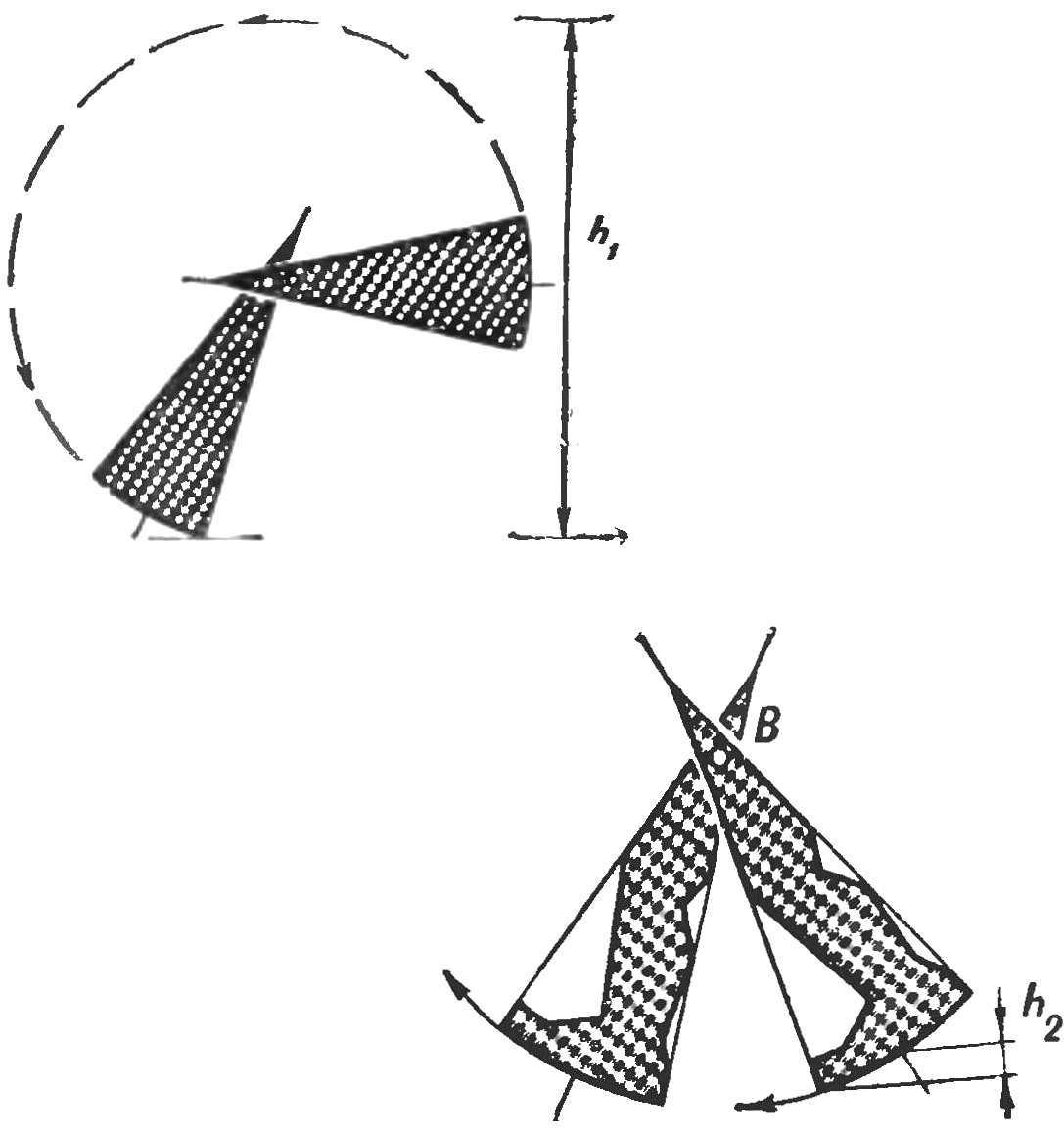
Рис. 1. Схема «шагания» — перемещения секторов.
В том и другом случае работа колеса, по сути дела, заменена движением лишь двух его секторов, то есть мы как бы облегчаем колеса, избавляемся от «лишних» его частей.
Но первый метод менее экономичен, так как сектор приходится поднимать выше и, кроме того, его холостой ход будет длиннее. Поэтому мудрая природа выбрала, например, для перемещения человека второй метод, предложив в качестве основной конструкции коленный и тазобедренный суставы — своеобразные шарниры.
Вернемся к нашей модели. Она снабжена оригинальным шагающим устройством, имеющим, помимо двух пар секторов, еще эксцентриково-кулисные механизмы. На шейки эксцентриков (рис. 2) установлены шариковые подшипники, внешние обоймы которых закреплены в специальных отверстиях секторов.
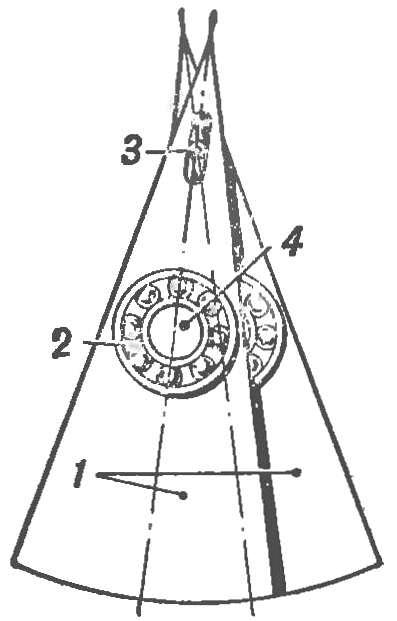
Рис. 2. Устройство секторов:
1 — секторы, 2 — подшипник, 3 — неподвижная ось кулисы, 4 — шейка эксцентрика ведущей оси.
В верхней части каждого сектора имеется продольный паз для оси кулисного механизма. Он заставляет секторы двигаться по определенной траектории, в результате чего модель совершает поступательное движение. Привод вала эксцентриков на модели может осуществляться от электромоторчика, питаемого от сети или батарей.
Чтобы модель двигалась плавно, без скачков, надо тщательно рассчитать размеры сектора. Делается это с помощью несложного геометрического построения.
РАСЧЕТ СЕКТОРОВ
Геометрическое построение дает возможность определить размеры и форму опорного башмака сектора. При этом мы находим соотношения величин радиуса эксцентрика, высоты расположения вала над опорной поверхностью и удаления от него оси кулисы.
Проведем две взаимно перпендикулярные оси ХУ и ВД (рис. 3). Из точки А, соответствующей центру вала эксцентрика, вниз откладываем отрезок АО, равный радиусу эксцентрика. Вверх из точки Д откладываем отрезок ДК, равный АО. Через точку К параллельно оси ХУ проводим линию ЕР. На горизонтальной оси, проведенной через точку А, откладываем отрезок АО1, равный радиусу эксцентрика. Из точки В (соответствующей положению неподвижной ОСИ кулисы) проводим прямую через точку О1 до пересечения в точке М с осью ХУ. Отрезок ОК откладываем от центра О1 вниз по линии ВМ и обозначим его О1К1. Восставим перпендикуляр из точки К1 до пересечения в точке с осью ХУ. Влево и вправо от точки К отложим на линии ЕР отрезки, равные K1L. Получим точки Е и Р, которые соединяем дугой через точку Д, в результате чего образуется сегмент ЕДР. Это и будет опорной частью сектора шагающего устройства, причем точки Р и Е показывают границы поверхности соприкосновения.
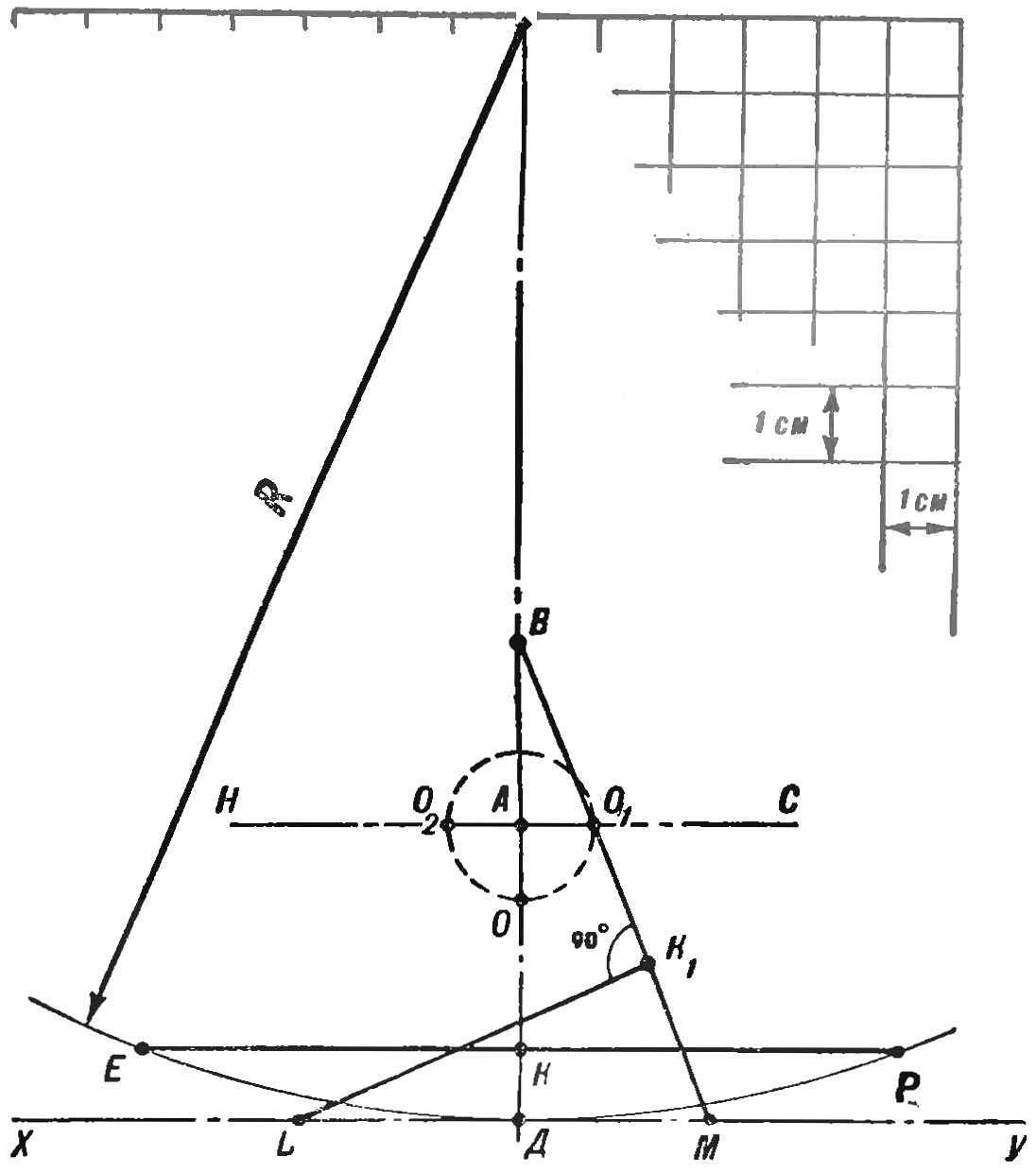
Рис. 3. Геометрические построения дуги для определения линейных размеров сектора.
Для получения более точной кривой соприкосновения, пользуясь приведенным методом, можем найти промежуточные точки дуги РЕ.
Размер опорной поверхности, или длина дуги РЕ, зависит от расстояния точки А до плоскости ХУ, радиуса эксцентрика АО и расстояния от ведущей оси А до неподвижной В. При изменении любой из этих величин размеры башмака изменяются. Следовательно, расположение осей и радиуса эксцентрика нужно подбирать в зависимости от требуемой длины н высоты шага движителя.